

你可能在日常生活中遇到过无数次这种只有一个面的物体——比如 the 通用回收标志,印在铝罐和塑料瓶的背面。
这个 数学对象 被称为莫比乌斯带。自1858年由德国数学家奥古斯特·莫比乌斯(August Möbius)发现以来,它一直让环保主义者、艺术家、工程师、数学家以及许多其他人着迷。这位数学家于150年前,也就是1868年9月26日去世。
1858年,莫比乌斯在担任莱比锡大学天文学和高等力学教授期间发现了这个单面带。(另一位名叫Listing的数学家实际上在几个月前就描述了它,但直到1861年才发表了他的研究成果。)莫比乌斯似乎是在研究多面体(由顶点、边和平面组成的立体图形)的几何理论时遇到了莫比乌斯带。
制作莫比乌斯带的方法是:取一条纸带,给它扭转奇数次半圈,然后将两端重新粘合起来形成一个环。如果你用铅笔沿着纸带的中心画一条线,你会发现这条线似乎同时在环的两侧延伸。
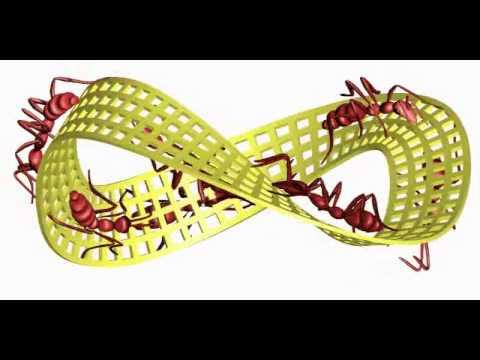
单面物体的概念启发了像荷兰图形设计师 M.C.埃舍尔 这样的艺术家。他的木刻版画《莫比乌斯带II》描绘了红蚂蚁在莫比乌斯带上一个接一个地爬行。
莫比乌斯带不仅只有一个令人惊讶的特性。例如,试着用剪刀沿着你刚才画的线将纸带剪成两半。你可能会惊讶地发现,你得到的不是两个较小的单面莫比乌斯带,而是一个长而双面的环。如果你手边没有纸,埃舍尔的木刻版画《莫比乌斯带I》展示了当莫比乌斯带沿着中心线被剪断时会发生什么。
虽然这种纸带无疑具有视觉吸引力,但它的最大影响在于数学领域,它促进了一个称为 拓扑学 的完整学科的发展。
拓扑学家研究的是物体在移动、弯曲、拉伸或扭曲时保持不变的性质,而不进行切割或粘合。例如,一团缠绕的耳机在拓扑学意义上与一团未缠绕的耳机是相同的,因为将一个变成另一个只需要移动、弯曲和扭曲。在它们之间转换不需要切割或粘合。
另一对在拓扑学上相同的物体是咖啡杯和甜甜圈。因为这两个物体都只有一个孔,所以一个可以通过拉伸和弯曲变成另一个。

物体的孔洞数量是一个只能通过切割或粘合才能改变的性质。这个性质——称为物体的“亏格”——使我们能够说,一对耳机和一个甜甜圈在拓扑学上是不同的,因为甜甜圈有一个孔,而一对耳机没有孔。
不幸的是,莫比乌斯带和一个双面环,比如普通的硅胶腕带,似乎都有一个孔,所以这个性质不足以区分它们——至少从拓扑学家的角度来看是这样。
取而代之的是,区分莫比乌斯带和双面环的性质称为可定向性。与孔的数量一样,物体的可定向性只能通过切割或粘合来改变。
想象一下在一个透明的表面上写下自己的便条,然后在这个表面上走一圈。如果当你从散步回来时,你总能读到这张便条,那么这个表面就是可定向的。在一个不可定向的表面上,你散步回来后可能会发现,你写的字似乎变成了它们的镜像,只能从右到左阅读。在双面环上,无论你的旅程去到哪里,便条总是可以从左到右阅读。
由于莫比乌斯带是不可定向的,而双面环是可定向的,这意味着莫比乌斯带和双面环在拓扑学上是不同的。

可定向性的概念具有重要的意义。例如对映体。这些化学化合物具有相同的化学结构,只有一个关键区别:它们是彼此的镜像。例如,化学L-甲基苯丙胺 是维克斯蒸气吸入剂的成分。它的镜像D-甲基苯丙胺是一种A类非法药物。如果我们生活在一个不可定向的世界里,这些化学物质将无法区分。
奥古斯特·莫比乌斯(August Möbius)的发现为研究自然世界开辟了新途径。拓扑学研究仍在不断产生惊人的结果。例如,去年,拓扑学引导科学家们发现了奇特的新物质状态。今年的菲尔兹奖,数学领域的最高荣誉,颁给了阿克谢·文卡塔什(Akshay Venkatesh),他是一位将拓扑学与其他领域(如数论)相结合的数学家。
David Gunderman是科罗拉多大学应用数学专业的博士生。Richard Gunderman是印第安纳大学医学、文科和慈善事业的校长教授。本文最初发表在 The Conversation。
